問題：Distinct elements

• 問題敘述：有 m 個數字輸入，每個數字介於[1, n]，希望可以輸出出現的「個別數字」

直觀方法

• n bits 的陣列，如果第i個進入就翻第 $n_{i}$ 的 bit 成1

• 儲存整個 stream，總計 m(lgn) 的bits

※ 在這兩種直觀方法，至少需要 O(min{n, mlgn}) 個bits

隨機估計

• 我們設定輸出為 $\tilde{t}$，並建立不等式： $\mathbf{P}(|t - \tilde{t}| > εt) < δ$
• 該方法由 Flajolet & Martin 提出，簡稱 FM

• 演算法：

  • 挑選隨機函數 $h：[n] → [0, 1]$
  • 獲得計算器 $X = min_{i \in stream} h(i)$
  • 輸出的值為 $\tilde{t} = \frac{1}{X} - 1$

• Claim 1.： $\mathbf{E}(X) = \frac{1}{t+1}$ 。直觀上，當t=1時，期望值為1/2，t=2，期望值會變為1/3，平均隨機分布。

• Claim 2.： $\mathbf{E}(X^2) = \frac{2}{(t+1)(t+2)}, Var(X) = \frac{t}{(t+1)^2(t+2)}$

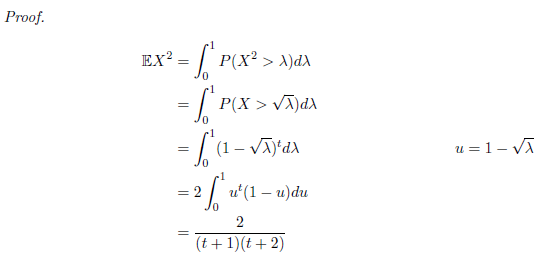
※這個時候，「FM」 還沒有任何結論

FM+

• 演算法：
  • 產生 $q = 1/ ε^2η$ 個獨立的 FM
  • 令 $X_{i}$ 為 FM 產生的值
  • 輸出的值為 $\tilde{t} = \frac{1}{Z} - 1$, $Z = \frac{1}{q}\sum_{i}X_{i}$
• $\mathbf{E}(Z) = \frac{1}{t+1}$ (不變)，$Var(Z) = \frac{1}{q}\frac{t}{(t+1)^2(t+2)} < \frac{1}{q(t+1)^2}$ (降低估計的變異數)
• Claim 3. ： $\mathbf{P}(|Z - \frac{1}{t+1}| > \frac{ε}{t+1}) < η$

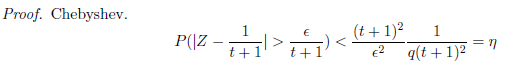
• Claim 4. ：$\mathbf{P}(|(\frac{1}{Z}-1)-t| > O(ε)t) < η$

※ 根據 Claim 3 ，邊界的 $Z = \frac{1\pm ε}{t+1}$

※ 這時已經可以透過控制 FM+ 的數量，限定出常數倍的「 $εt$ 」的邊界

FM++

• 演算法：

  • 產生 $s = \lceil 36 ln(2/δ) \rceil$ 個獨立的 FM+
  • 輸出的值為 $\tilde{t}$ 為 $s$ 個 $\frac{1}{Z_{j}} - 1$  的中位數

• Claim 5. ：$\mathbf{P}(|\tilde{t}-t| > εt) < δ$

  • 若是中位數失敗，則代表有過半數的 $Y_{j}$ 都失敗 → $\sum_{j=0}^{s} Y_{j} > s/2$
  • 令 $\mathbf{E}(Y_{j}) = \frac{s}{3}$ (平均有 $\frac{1}{3}$ 的失敗機率)
    • $\mathbf{P}(\sum Y_{j} > s/2 ) = \mathbf{P}(\sum Y_{j} - s/3> s/6) = \mathbf{P}(\sum Y_{j} - \mathbf{E}(\sum Y_{j}) > \frac{1}{2}E(\sum Y_{j}))$
    • (use Chernoff) $< 2‧e^{-\frac{(\frac{1}{2})^2s/3}{3}} < δ$

※ (→) 可以推出需要多少 s 個 FM++ 才能符合邊界

FM++空間

• 不考慮 FM 裡的 h 空間，總共需要 $O(q*s) = (1/ ε^2η)*\lceil 36 ln(2/δ) \rceil = O(\frac{lg(1/δ)}{ε^2})$
• 有 $O(lg(1/δ))$ 個 FM+，每個需要 $O(\frac{1}{ε^2})$ 空間

(補充)

k-wise independent function

• 定義：當一個函數家族 family $H$ ：[a] → [b] 是 「k-wise independent」，指不重複 $\forall i1,...,ik \in [a]$ 可以對應到 $\forall j1,...,jk \in [b]$ ：

$$\mathbf{P}_{h \in H}(h(i_{1})=j_{1} \wedge ... \wedge h(i_{k})=j_{k}) = \frac{1}{b^k}$$

• 代表意義：任意 k 組 i → j 的映射函數被選中機率相等

• 例子1： $H$ 為在每個 k 值， 是 [a] → [b]的映射函數且具有「k-wise independent」特性的函數集合。

  • $|H| = b^a$ ，代表 $h$ 需要 $lg(b^a) = alg(b)$ 的bits儲存

• 例子2：令 $a = b = q,q = p^r$ (質數的次方)。 $H_{poly}$ 是指最高次方 $\leq k-1$ 且固定係數的多項式集合。

  • $|H_{poly}| = q^k$ ，最多有k項，每項的值 $\in [q]$ ，代表 $h$ 需要 $lg(q^k) = klg(q)$ 的bits儲存
  • $H_{poly}$ 也是 「k-wise independent」

Non-idealized FM

• 原因：idealized FM，隨機數值取無理數且不儲存stream裡的值

首先，我們使用 O(1) 的複雜度估計 O(lg n) bits，例如使估計值 $\tilde{t}$ 滿足 $t/C \leq \tilde{t} \leq Ct$，$for$ 常數 $C$

• 演算法：
  • 從 2-wise family $[n] → [n],(n是2的次方)$ 挑選出一個函數 $h$
  • 使 $X = max_{i \in str }lsb(h(i))$ → $lsb(X) = min \ [bit(X) \neq 0]$
  • 輸出的值為 $2^X$

• 推導：

  • 令 $Y_{i} = [lsb(stream(i)) = j]$
  • 令 $Z_{j} = \sum_{i=1}^{L} Y_{i}, \quad Z_{>j} = \sum_{i=1}^{L} [lsb(stream(i)) > j]$
    • $\mathbf{E}[Z_{j}] = t/2^{j+1}$
    • $\mathbf{E}[Z_{>j}] = t(\frac{1}{2^{j+2}} +\frac{1}{2^{j+3}}+...) < t/2^{j+1}$
    • $Var[Z_{j}] < t/2^{j+1}$
      • $Var[\sum Y_{i}] = \mathbf{E}[\sum Y_{i}]^2-(\mathbf{E}[\sum Y_{i}])^2$
      • $=\sum_{i=1}^{t}\mathbf{E}[Y_{i}^2] + \sum_{i\neq j}\mathbf{E}[Y_{i}Y_{j}]-(\mathbf{E}[\sum Y_{i}])^2$
      • $=t/2^{j+1}+(t^2-t)/(2^{j+1})^2-t^2/(2^{j+1})^2 =t/2^{j+1}-t/(2^{j+1})^2 < t/2^{j+1}$

  • 邊界：

    • 現在令 $j^{-} = \lceil lg(t) - C_{1} \rceil$
      • $\Rightarrow 2^{C_{1}-1} \leq \mathbf{E}Z_{j^{-}} \leq 2^{C_{1}}$
      • $\Rightarrow \mathbf{P}(Z{j^{-}} = 0) \leq \mathbf{P}(|Z_{j^{-}}-\mathbf{E}Z_{j^{-}}| \geq 2^{C_{1}-1})$
      • (using Chebyshev)$\Rightarrow < \frac{t/(t/2^{C_{1}-1})-t/(t/2^{C_{1}-1})^2)}{(2^{C_{1}-1})^2} = \frac{1}{2^{C_{1}-1}}-\frac{1}{t} < \frac{1}{2^{C_{1}}}$
      • 證明：比 $lg(t) \; 少 \;C_{1}$位一個都沒有出現的機率很低

    • 現在令 $j^{+} = \lceil lg(t) + C_{2} \rceil$

      • $\Rightarrow \mathbf{E}Z_{>j^+} < 1/(2^{C_{2}+1})$
      • (using Markov) $\Rightarrow \mathbf{P}(Z_{>j^+} \geq 1) < 1/(2^{C_{2}+1})$
      • 證明：比 $lg(t) \; 多 \; C_{2}$ 位以上出現的機率很低

• 結論：可以將 $lsb(t)$  出現的範圍限定在 $lg(t)$ 兩個常數邊界 $[-C_{1},+C_{2}]$，可以有效估計最大 $max \; lsb(t)$  與 $lg(t)$ 的誤差

Refine to 1+ε

• Trivial Solution：演算法 "TS" 儲存前 $C/ε^2$ 不重複元素。當 $t \leq C/ε^2$ 時會保證一定正確。
• 演算法：
  • 產生 $TS_{0},...,TS_{lg(n)}$
  • 從 2-wise family $g: [n]→[n]$ 選擇一個函數
  • 將 i 輸入進 $TS_{lsb(g(i))}$ 中
  • 輸出的值為 $2^{j+1}\;‧out(TS_{j})$  當 $t/2^{j+1} \approx 1/ε^2 \Rightarrow 代表\;index \;j\;裡面的值是較符合期望值$
• 推導：
  • 令 $B_{j}$ 為 $TS_{j}$裡不重複元素的個數
  • $\mathbf{E}B_{j} = t/2^{j+1}=Q{j} \Rightarrow B_{j} = Q_{j} \pm O(\sqrt{Q_{j}})$在還不錯的機率 (using Chebyshev)
  • $= (1\pm O(ε))Q_{j} \quad(如果\; Q_{j} \geq 1/ε^2)$
• 需要的空間：$\frac{C}{ε^2}(lg\; n)^2=O(\frac{1}{ε^2}lg^2\;n)$