問題：Approximate Counting

• 第一篇關於 Streaming 的論文
• 問題敘述：當有一連串事件發生後，我們希望計算事件發生的數量，並且盡量節省計算上的空間使用。
• 最簡單且直覺的做法：若有n筆事件，則計算器至少需要 (lg n) 個 bits 才有足夠空間儲存 0~n 的值。
• 在「估計計算問題」裡，我們希望估計值 n' 可以符合下列的不等式：(通常ε=1/3, δ=1%)

$$\mathbf{P}(|\tilde{n}-n| > εn ) < δ$$

因為估計時只需要判斷目前數量坐落在 2的次方 中的哪個區間，故只需 (lg(lg n)) 個 bits 就可以了判斷 (lg n) 個邊界。

Morris Algorithm

演算法：

• 初始化 X 為 0
• 對每個事件，以$\frac{1}{2^X}$的機率增加X
• 輸出的估計值 $\tilde{n} = 2^X -1$

以下是Wiki pedia裡面的算法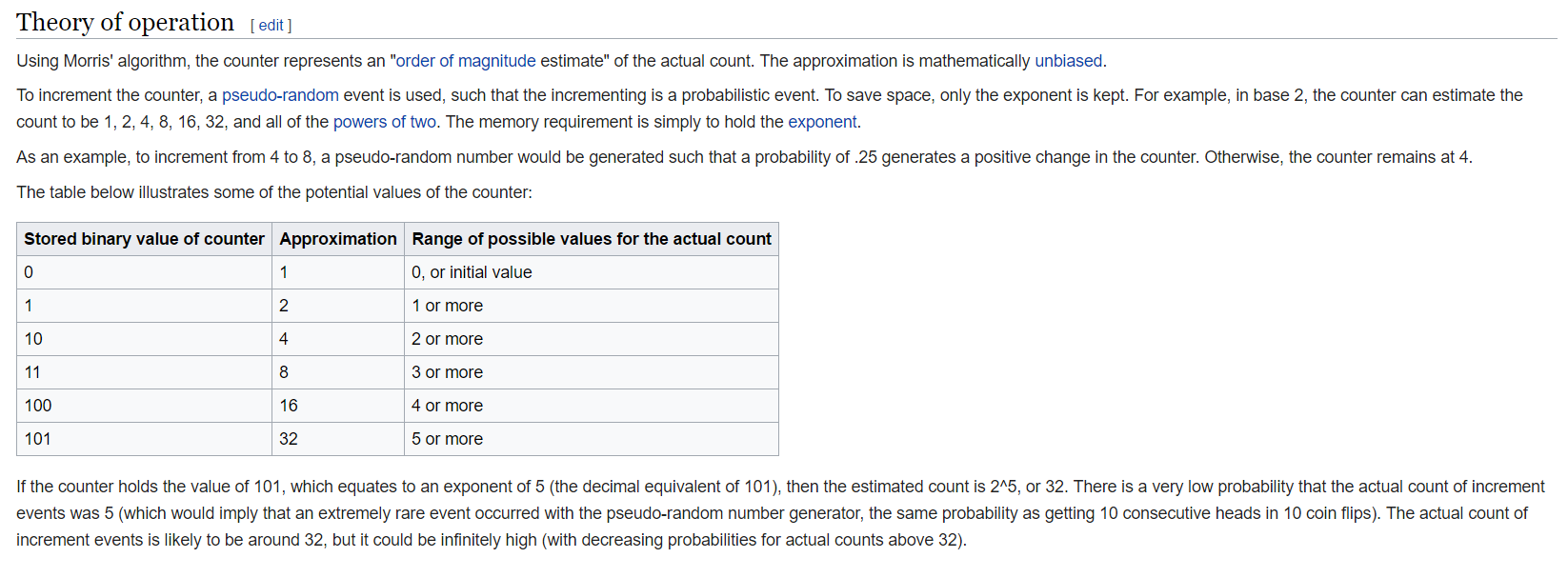：計算方式：當一個事件發生時，隨機產生一個低機率觸發計算器增倍，因為機率的關係所以事件的數量會接近期望值。

以下為機率複習

• Lemma 1：$\mathbf{E}(X+Y) \ = \mathbf{E}(X) \ +\ \mathbf{E}(X) \, \rightarrow \,$ 顯而易見
• Lemma 2 (Markov)：當X是非負的隨機變數時

$$\forall λ > 0, \mathbf{P}(X > λ ) < \frac{\mathbf{E}(X)}{λ}$$

• Lemma 3 (Chebyshev)：處理變異數相關的邊界

$$\forall λ > 0, \mathbf{P}(|X - \mathbf{E}(X)| > λ ) < \frac{\mathbf{E}(X - \mathbf{E}(X))^2}{λ^2} = \frac{Var(X)}{λ^2}$$

• Lemma 4 (Chernoff)， $X_{1}到X_{n}$都是隨機的獨立變數，且$X_{i} \in [0,1]$，使 $X = \sum_{i=0}^{n} X_{i}, λ > 0：$

$$\mathbf{P}(|X-E(X)| > λ．\mathbf{E}(X)) \le 2．e^{-λ^2．E(X)/3}$$

• Lemma 5 (Bernstein)：$X_{1}到X_{n}$都是隨機的獨立變數，且 $|X_{i}| \le K$ 。For $\forall t ＞ 0$：

$$\mathbf{P}(|X-\mathbf{E}(X)| > t ) \le e^{-ct^2/σ^2} + e^{-ct/K}$$

(c是常數)

將「機率」應用在「分析」上

• $X_{n}$  被設為 $X$ 在 Morris Algorithm 經過 n 事件後的值
• Claim 6

$$\mathbf{E}(2^{X_{n}}) = n + 1$$

推倒過程

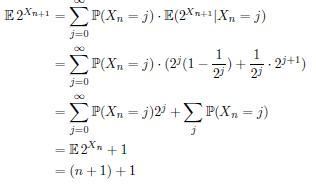
※解釋：Xn 為區間值

※解釋：前項 $2^j(1-\frac{1}{2^j})$ 為沒有取中，後項 $\frac{1}{2^j}‧2^{j+1}$ 為取中

• Claim 7：用 Lemma 3 產生 $\tilde{n}$ 的邊界

$$\mathbf{P}(|\tilde{n} - n | > εn) < \frac{1}{ε^2‧n^2}‧\frac{n^2}{2} = \frac{1}{2ε^2}$$

Morris+ & Morris++

• Morris+：若是 $\tilde{n}$ 估計的失敗機率需小於一個特定的值 (如1/3)，則可以增加成s倍的Counter再將輸出取平均，就可以將誤差降低。反推回去便可知需要多少數量的 Counter

• Morris++：將Morris+中的中位數拿來判斷，若Morris+的中位數失敗，就代表有一半的Morris+失敗